Как посчитать площадь комнаты в квадратных метрах и её квадратуру стен?

Как рассчитать площадь комнаты стандартной формы

Под площадью комнаты подразумеваются числовые характеристики, которые показывают её размер в двухмерном пространстве. Если комната стандартная (прямоугольная или квадратная), то сделать расчёт легко. Нужно только померить длину и ширину. Делается это вдоль стен по полу, при загроможденности данных участков, возможно, проводить замер посредине комнаты.

Важно, одна сторона должна измеряться строго перпендикулярно второй. Стороны расположенные параллельно должны иметь один размер, но несмотря на это, меряются обе

Кроме того, следует проверить правильность формы, то есть провести промеры диагоналей. В прямоугольном или квадратном помещении, они должны равняться, или иметь небольшие отклонения.

Квадратное помещение

Как рассчитать S квадратных помещений — это довольно легко. У квадратной комнаты все стороны равны.  Однако, как говорилось выше, надо замерить их все, и взять средне арифметический показатель для расчёта:

А — размер сторон.

Рассмотрим пример: комната со стенами по 3 метра, 3 в квадрате — S = 9 м2.

Прямоугольное

Рассчитать площадь помещений прямоугольной конфигурации, также легко путём следующих вычислений:

На примере видно, при ширине 4,10 м, длине 6,15 м, S комнаты получается — 4,10 x 6,15 = 25,215 м2. После запятой оставляется две цифры, остальные округляются, то есть выходит 25,22 м2.

4 Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

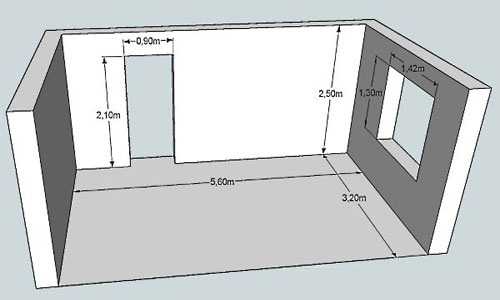Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

4.1 Как измерять стены с дверью и окном?

Если в комнате есть окно или дверь, то для получения актуальных показателей их необходимо обязательно измерить. Воспользовавшись все той же рулеткой, узнайте высоту и ширину оконного проема, умножьте один результат на другой и вычтите это произведение из общей площади. Не надейтесь на то, что их форма является правильной.

Приведем пару примеров.

Пример 1. Стена с дверным проемом:

• Общая S стены – 2,7 м х 8,0 м = 21,6 м2;
• S дверного проема в стене – 2,3 м х 0,9 м = 2,07 м2;
• S стены без дверей – 21,6 м2 – 2,07 м2 = 19,53 м2.

Пример 2. Стена с оконным проемом:

• Общая S стены – 2,4 м х 5 м = 12 м2;
• Площадь окна – 1,4 м х 1,65 м = 2,24 м2;
• S стены без окна – 12 м2 – 2,24 м2 = 9,76 м2.

4.2 Что нужно, чтобы рассчитать площадь стен?

Рассчитать площадь стен дома можно либо онлайн, либо вручную. Второй вариант более трудоемкий, но точный и подходит в случае, если нет доступа к интернету по тем или иным причинам. Для расчетов потребуется:

• карандаш или ручка;
• листок бумаги;
• калькулятор;
• длинная линейка;
• уровень;
• рулетка.

Важно! Зная точную площадь стен и помещения, можно приобрести нужное количество строительных материалов, необходимых для ремонта. Площадь измеряют квадратными метрами и обозначают м2

На бумаге делается чертеж комнат, обозначаются окна, двери, ниши, все выступы. И по мере получения замеров, их наносят на чертеж.

4.3 Как посчитать квадратные метры стены с окном

Сложнее будет иметь дело со стеной, на которой расположено окно.

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Алгоритм действий:

1. По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
2. Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
3. Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах

4.4 Как посчитать квадратные метры стены с дверью

Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.

Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.

1 Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

1.1 Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

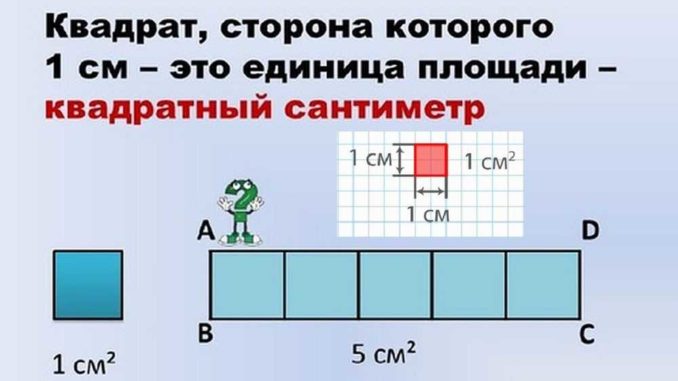Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м².  В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

1.2 Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

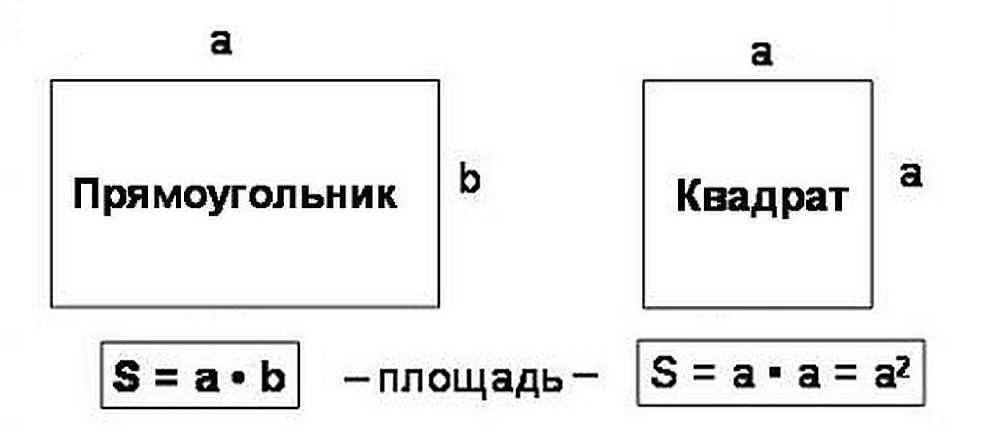При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

1. Имеем прямоугольник со сторонами 80 см и 50 см. Перемножаем эти цифры: 80 * 50 = 4000 см². Это и будет его площадь.
2. Стороны 322 см и 300 см. Получим: 322*300 = 96000 см².
3. Есть квадрат со стороной 60 см. Его площадь — 60 * 60 = 3600 см².

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Простейший калкулятор для расчета площади прямоугольной комнаты.

a =

b =

1.3 Перевод квадратных сантиметров в квадратные метры

Когда имеем дело с сотнями сантиметров, удобнее и проще считать в метрах. Мы знаем, что в одном метре сто сантиметров. Давайте решим те же примеры, но переведем сантиметры в метры:

1. 80 см = 0,8 м; 50 см = 0,5 м. Перемножаем 0,8*0,5 = 0,4 м². То есть, 0,4 квадратных метра.
2. 322 см это 3,22 м; 300 см это 3 м. Теперь умножаем полученные цифры: 3,22 * 3 = 9,6 м².
3. 60 см равны 0,6 м. Площадь квадрата с такой стороной 0,6*0,6 = 0,36 м².

Цифры получаются намного меньше, запомнить их проще. И если мы хотим посчитать площадь комнаты в квадратных метрах, ее размеры мы меряем в метрах, а не сантиметрах. Можно перевести квадратные сантиметры в квадратные метры. Как уже говорили, в одном квадратном метре содержится десять тысяч квадратных сантиметров.

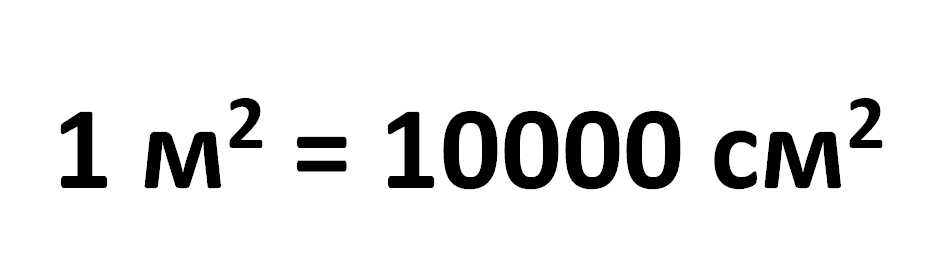Соотношение квадратных сантиметров и квадратных метров

Если же у вас есть площадь в квадратных сантиметрах, чтобы перевести ее в квадратные метры, цифру надо разделить на 10 000. Например:

• 4000 см² / 10000 = 0,4 м²;
• 96000 см² / 10000 = 9,6 м²;
• 3600 см²/ 10000 = 0,36 м².

Как видите, все просто. Надо только запомнить основные положения и посчитать площадь комнаты в квадратных метрах будет совсем несложно. Нужно будет предварительно провести измерения, а потом заняться расчетами.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Алгоритм проведения расчётов

Если все подготовлено, то можно переходить к самим расчётам. Если нужно вычислить площадь поверхности правильной формы, то здесь нет ничего сложного – эти формулы уж точно никто не позабудет.

Без рулетки никакИсточник sv.decorexpro.com

Другое дело, когда стена, пол, потолок имеют сложные очертания. Здесь уже придётся сочетать различные приёмы. То есть поделить комнату на несколько блоков, после чего рассчитать площадь каждого из них. А далее от общей площади вычесть или прибавить их.

Вовсе не обязательно мерить длину стен строго вдоль плинтусов – замер можно проводить в любом удобном месте, если, скажем, мешает мебель. То есть выше, ниже, в середине, главное соблюсти при этом строгую параллель полу и потолку. Никаких диагоналей или наклонов! В противном случае расчёты будут неверными.

При возникновении трудностей можно всегда заручиться поддержкой кого-то из домашних.

Правильная геометрия

Каких-либо сложностей касательно того, как вычислить площадь, здесь нет. В случае простого прямоугольника достаточно замерить всего две стороны и высоту, ведь у такой фигуры противоположные стороны равны. Чтобы убедиться, что комната имеет правильные очертания, достаточно приложить к углам строительный угольник, правда не всегда удаётся получить чёткую картину.

Формула для расчёта прямоугольника известна каждому:

S=a⋅b, где:

• S – рассчитываемая площадь;
• a – длина;
• b – ширина.

Кажется, что формулу площади прямоугольника забыть невозможно, хотя у некоторых получается и этоИсточник wezanu.ritobypus.ru.net

Такая формула актуальна для стен, потолка, пола, дверей, окон и прочих прямоугольных поверхностей

В случае запланированного ремонта важно получить чистые значения. Для этого следует от площади стены вычесть площадь дверей, окон

Общую площадь всей комнаты можно рассчитать по такой формуле – h(a⋅2+b⋅2). Где h – высота помещения.

С квадратом все ещё проще – достаточно замерить одну сторону и возвести её значение в квадрат.

Помещения с неправильными очертаниями

Но как посчитать площадь комнаты, если она имеет неправильную форму поверхностей? Здесь есть некоторые нюансы:

• Стены. В мансардной комнате стена может иметь форму трапеции или треугольника.
• Потолок. В тех же мансардных помещениях данная плоскость может быть под определённым углом. Также есть варианты с ломаной поверхностью, когда несколько плоскостей пересекаются межу собой.

Но ничего страшного здесь нет и не нужно углубляться в тригонометрию. Достаточно любую сложную поверхность стен или потолка визуально разделить на несколько простых плоскостей. После этого остаётся рассчитать площадь каждой фигуры и сложить их вместе.

Случай чуть-чуть посложнее – но не намногоИсточник wezanu.ritobypus.ru.net

Для облегчения ниже приведём несколько формул площадей, которые могут пригодиться:

Круг:

• S=π⋅R² – нужен только радиус.
• Сектор круга определятся так – S=0,5pr.

Параллелограмм:

• S=a⋅b⋅sin(α) – по двум сторонам и углу между ними.
• S=a⋅h – по высоте и основанию.

Треугольник:

• S=0,5⋅b⋅h – по основанию и высоте.
• S=0,5⋅ab⋅sin(α) – по сторонам и углу.
• S=√(p·(p-a)·(p-b)·(p-c)) – формула Герона по трем сторонам.

Трапеция:

• S=0,5⋅h⋅(a+b) – по высоте и основанию.
• S=m⋅h – по средней линии и высоте.

Эллипс:

• S = π⋅R1⋅R2 – по двум радиусам R1 и R2
• S=π⋅a⋅b – через полуоси a и b.

Обозначения: π – 3,14159 (всем известное число пи), R – радиус, a, b, c – стороны фигуры, p – полупериметр (для формулы Герона), h – высота, m – средняя линия.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

Схема комнаты с нанесенными измерениями

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

• Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
• Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
• Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

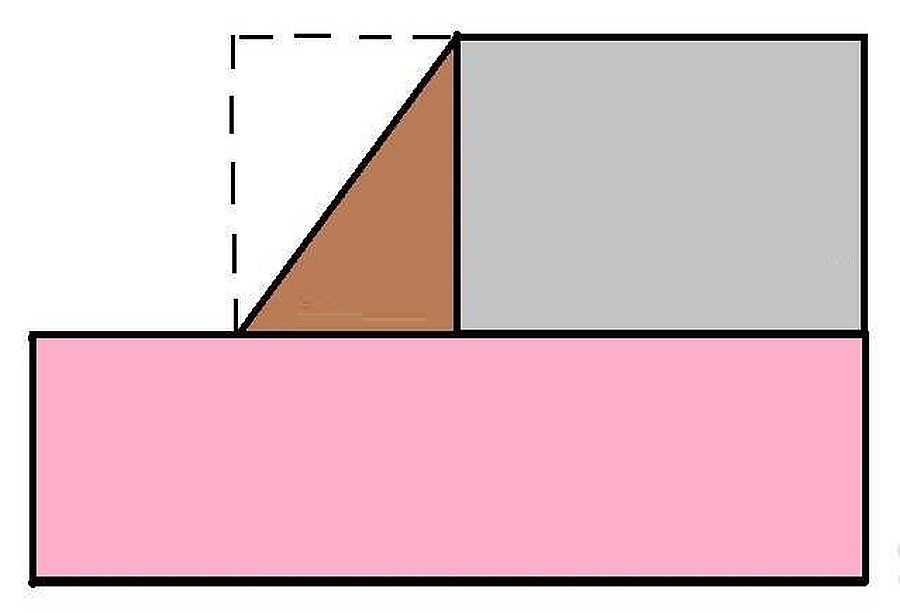Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

• Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
• Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м².  Снова округлим до 0,67 м².
• Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
• Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

https://youtube.com/watch?v=YL07nZH5ueY

Как рассчитать площадь потолков и стен

Пло­щадь потол­ка обыч­но рав­на пло­ща­ди пола, за исклю­че­ни­ем мно­го­уров­не­вых потол­ков, поэто­му отдель­но её вычис­лять не требуется.

S стен необ­хо­ди­ма чаще все­го для опре­де­ле­ния коли­че­ства кера­ми­че­ской плит­ки или руло­нов обоев.

• Если обо­я­ми или плит­кой закры­ва­ет­ся все сте­ны, то про­ще вна­ча­ле рас­счи­тать общий пери­метр поме­ще­ния Р, сло­жив все дли­ны его стен. Р = 2 * (а + b).
• Затем Р нуж­но умно­жить на высо­ту стен h. Полу­ча­ем сум­мар­ную пло­щадь всех стен S.
• Теперь из S стен вычи­та­ет S окон и двер­но­го про­ема, пред­ва­ри­тель­но рас­счи­тан­ных по фор­му­ле (1).

Таким обра­зом S под отдел­ку опре­де­ля­ет­ся по такой фор­му­ле: S отд. = (2 * (а + b) * h) — S окон — S две­рей (6).

Если про­из­во­дит­ся частич­ная отдел­ка, то рас­счи­ты­ва­ет­ся пло­щадь поверх­но­сти сте­ны, пред­на­зна­чен­ной для отделки.

При­мер, как най­ти пло­щадь S отд. для сте­ны с дверью:

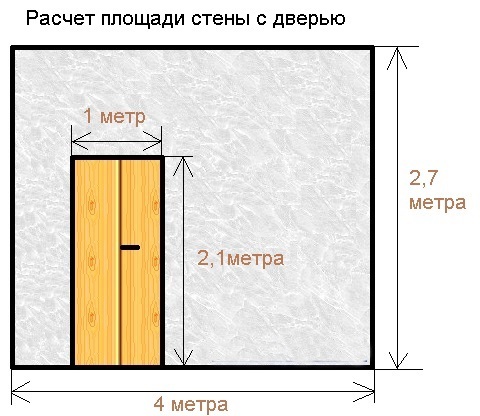
S отд. = S сте­ны – S две­ри = 4 * 2.7 – 1 * 2.1 = 8.7 м2.

 Как высчитать, сколько нужно плитки для фартука

• Что­бы выло­жить фар­тук из плит­ки на кухне, нуж­но вна­ча­ле про­из­ве­сти его раз­мет­ку и заме­рить дли­ну и высоту.
• Затем по ф‑ле (1) рас­счи­ты­ва­ем пло­щадь фартука.
• Для рас­че­та коли­че­ства плит­ки необ­хо­ди­мо S фар­ту­ка раз­де­лить на S одной плит­ки: N пл. = S фарт. / S пл. одной плит­ки (7).
• К рас­чёт­но­му коли­че­ству N нуж­но при­ба­вить ещё 5 — 10%, с учё­том нарез­ки угло­вых пли­ток и неиз­беж­но­го части мате­ри­а­ла в рас­ход (часть плит­ки бра­ку­ет­ся плиткорезом).

То есть ито­го­вое коли­че­ство будет рав­но: N итог. = N пл. + N пл. * (0.05 — 0.1) (8).

Коли­че­ство плит­ки для ван­ной, если ею закры­ва­ют­ся все сте­ны, рас­счи­ты­ва­ет­ся по мето­ду, опи­сан­но­му выше:

• по фор­му­ле (6) рас­счи­ты­ва­ем S отде­лоч­ной поверх­но­сти стен.;
• по ф‑лам (7) и (8) — коли­че­ство плитки.

Как посчитать количество обоев

Рас­чёт необ­хо­ди­мо­го коли­че­ства обо­ев более сло­жен, так как необ­хо­ди­мо учитывать:

• шаг узо­ра обоев;
• запас на отрез.

Коли­че­ство руло­нов счи­та­ют дву­мя способами:

• по пло­ща­ди стен;
• по пери­мет­ру поме­ще­ния и коли­че­ству полотен.

Суще­ству­ют гото­вые таб­ли­цы рас­че­тов обоев.

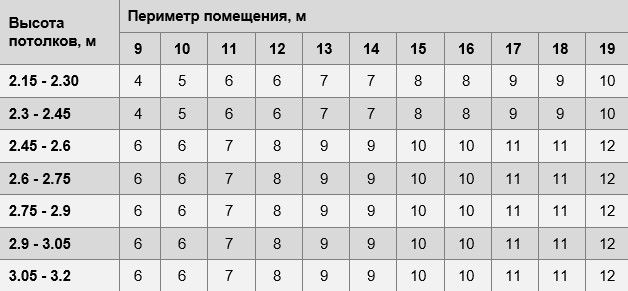
Первый способ расчета

Пер­вый спо­соб про­стой, но он весь­ма при­бли­зи­тель­ный, поэто­му при­хо­дит­ся поку­пать обои с боль­шим запа­сом, что неэкономно.

• Рас­счи­ты­ва­ет­ся пло­щадь поверх­но­сти отдел­ки S отд. за выче­том окон и две­рей — по ф‑ле (6).
• Опре­де­ля­ет­ся пло­щадь одно­го руло­на: дли­на руло­на умно­жа­ет­ся на его шири­ну. Напри­мер, если в рулоне шири­ной 60 см 10 мет­ров полот­на, то S одно­го руло­на будет 6 м2.
• Затем делим S отд. на S одно­го руло­на, и полу­чен­ную циф­ру округ­ля­ем до цело­го числа.
• При­бав­ля­ем один — два руло­на в запас.

Второй способ расчета

Вто­рой спо­соб более точен и эко­но­мен, но и более сложен:

• Высчи­ты­ва­ем пери­метр части поме­ще­ния Р, без окон­ных и двер­ных про­емов, на кото­рые пой­дут целые полотна.
• Опре­де­ля­ем дли­ну одно­го цело­го полот­на l ц.: к высо­те поме­ще­ния (обыч­но 2.60 м) при­бав­ля­ем запас на узор 0.5 м и на отрез — 0.1 м.
• Высчи­ты­ва­ем коли­че­ство целых поло­тен N ц., раз­де­лив Р на l ц.
• Теперь рас­счи­та­ем таки­ми же спо­со­ба­ми дли­ну l к. и коли­че­ство N к. кус­ков поло­тен над окна­ми, две­ря­ми и под окнами.
• Опре­де­ля­ем общий мет­раж целых поло­тен L ц. = N ц. * l ц.
• Высчи­ты­ва­ем, сколь­ко все­го мет­ров будет выре­зан­ных кус­ков L к. = N к. * l к.
• Рас­счи­ты­ва­ем общую дли­ну поло­тен: L общ. = L ц. + L к.

Теперь необ­хо­ди­мо посчи­тать сколь­ко все­го руло­нов нуж­но. Для это поде­лим L общ. на дли­ну одно­го руло­на, а полу­чен­ную циф­ру округ­лим в сто­ро­ну увеличения.

При срав­не­нии обе­их спо­со­бов рас­че­та обыч­но наблю­да­ет­ся раз­ни­ца в один рулон. Если не хочет­ся мучить­ся со вто­рым мето­дом, мож­но посту­пить про­ще: опре­де­лить коли­че­ство руло­нов по пер­во­му спо­со­бу и доба­вить про запас не два руло­на, а один.

Про­из­ве­дя рас­чет обо­ев, мож­но срав­нить теперь полу­чен­ную циф­ру с табличной.

Таким обра­зом реше­ние про­стой зада­чи как посчи­тать пло­щадь поме­ще­ния пред­став­ля­ет не толь­ко прак­ти­че­ский инте­рес, но и явля­ет­ся непло­хой тре­ни­ров­кой для моз­га. Само­сто­я­тель­ный рас­чет коли­че­ства отде­лоч­но­го мате­ри­а­ла поз­во­ля­ет не допу­стить его перерасход.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Как рассчитать площадь пола?

Итак, как же рассчитать квадратные метры? Самыми простыми для формулировки площади пола, является дом квадратной и прямоугольной формы. Чтобы провести расчет площади подобного помещения, необходимо измерить длину и ширину комнаты (измеряем в метрах), а потом умножить эти два числа друг на друга, получив интересующее нас число. Такой вариант не трудно осуществить, не требуется перестановка дивана, шкафа и прочей мебели – хватит всего лишь, посчитать расстояние. Единственной проблемой, будет камин (если он, конечно же, есть) в таком случае от итоговой цифры, необходимо будет вычесть S (площадь) камина.

Комнаты неправильной формы, представляют более сложный расчет S пола. Квартира, имеющая форму прямоугольника или квадрата, называют стандартной, однако, если есть наличие декоративных изменений (арок, ниш), то подсчет более сложный, поскольку требует вычисление S фигур входящих в состав комнаты.

Сначала план нужно разделить на два прямоугольника, а затем суммировать их площади

Вычисляя итоговую площадь «нестандартных фигур», например, Г-образную комнату, можно «разбить» помещение на два квадрата или треугольника и суммировать их сумму, такая небольшая хитрость позволяет в считаные минуты без каких-либо математических формул расчета, узнать S данного участка. В некоторых случая, угол Г-образной комнаты переходит не под углом 90º, что является небольшой, но решаемой загвоздкой. Пересекаясь под непрямым углом, переход имеет вид треугольника, расчет нужно провести, по знакомому геометрическому закону: «Площадь треугольника, равна первому катету умноженному на второй».

Цилиндрические и полусигментные частицы, но как же вычислить квадратные метры исходя из базового курса алгебры и геометрии? Гораздо легче, разделить участок на условные треугольники и квадраты, а затем сделать расчет и суммирование результатов каждого отдельного элемента.

Формулы площади, геометрических фигур

Существуют гостиные комнаты в частных домах, имеющие различную высоту пола (выступы, возвышенности, уклоны). Чтобы выполнить расчет, необходимо, как и прошлом случае разделить области на отдельные элементы, измеряв каждый по отдельности суммировав результаты.

Рулетка – это лучший инструмент, который поможет высчитать S пола. Однако, помимо рулетки необходимо взять листик и карандаш и записать замеры, а лишь потом проводить математические вычисления (чтобы не запутать и не перемерять все по десять раз).

Совет

Не осуществляйте замеры по стене, поскольку, она может иметь дефекты и привести к неточности измерения. Места, имеющие выступы в виде полукругов или зигзагов – следует считать по отдельности.

Треугольники

Проще всего иметь дело с прямоугольными представителями этого семейства. Начертив его на бумаге, несложно заметить, что он составляет половину прямоугольника. Соответственно и формула расчёта отличается незначительно: S=a*b/2. Где под буквами a и b подразумевается длина катетов (сторон, соприкасающихся под прямым углом).

Если треугольник не имеет прямых углов, необходимо провести следующие действия:

• принять одну из его сторон за основание;
• провести от вершины к нему высоту;
• умножить одно на другое;
• результат разделить на 2.

В итоге формула будет иметь такой вид: S=a*h/2. Где a и h — длина основания и высота соответственно.

Для любителей экзотики существуют и другие варианты. Например, формула Герона, или подсчёт с помощью радиуса вписанной в треугольник окружности. Но проще всё-таки будет считать через основание и высоту.

Круги и овалы

Такие геометрические формы в строительстве встречаются редко, но всё же встречаются. Чтобы рассчитать площадь круга достаточно найти его радиус и подставить в уравнение: S=πr2. Оно известно нам ещё со школы. И, если верить учебникам, r — это радиус круга, а величина π равна 3,14.

Площадь овала (эллипса) вычисляется похожим образом. Только вместо радиуса необходимо найти длину двух его полуосей — длинной (a) и короткой (b). Дальше — по той же схеме: S=π*a*b.

Но чаще можно столкнуться с полукруглыми или «полуовальными» помещениями. Для подсчёта размеров такой комнаты к формулам для круга и овала в конце дописываем /2. На латыни это будет выглядеть так: S=πr2/2 и S=π*a*b/2.

Заключение

Подобная точность расчетов на конечный результат особо не влияет, поскольку мало кто приобретает облицовочные материалы исходя из подобных расчетов. Как правило, приобретают любые облицовочные материалы с некоторым запасом. Если, например, считают количество керамической плитки, то расчеты производят по количеству штук, исходя из схемы укладки. Даже в этом случае, ее берут с некоторым избытком. Это связано еще и с тем, что возможны нештатные ситуации, связанные с порчей облицовочного материала. Особенно это актуально, когда работы выполняются самостоятельно, без привлечения профессионалов.

Это относится и к таким материалам, как обои, линолеум, ламинат, различная вагонка, сайдинг и т.д. Нужно всегда помнить, что при работах появляются отходы и, причем, их может быть немало, если размеры произвольные, без учета применения тех или иных материалов.

Подобный подход особенно актуален при укладке линолеума, который имеет стандартные размеры по ширине. Что касается его длины, то тут нужно очень точно все измерить и всегда сантиметров 10, но добавить. Если просчитаться, то это может дорого обойтись.

Математика 4 класс. 11 октября. Площадь и метр квадратный

Watch this video on YouTube